技术征文第4期：FastSPICE矩阵实现（概伦电子篇）--中国石油大学--“我为祖国献石油”队

一、活动背景

集成电路EDA设计精英挑战赛国内首个EDA领域专业赛事，赛题覆盖EDA应用及算法，从本科到博士都可参赛，需具备计算机、电子、物理、数学等知识储备，对参赛队伍的要求极具综合性。通过2届大赛的举办，受到了来自产业及高校的高度关注，产业界和学术界专家反馈，参赛作品具有很好的参考和学习价值，继第一届后现选出第二届优秀作品并参与技术征文投稿的队伍作品和大家分享

二、团队介绍

队伍名称：我为祖国献石油

队伍成员：伊恩鑫、段懿洳、周浩楠

所在学校：中国石油大学（北京）

获奖情况：2020第二届集成电路EDA设计精英挑战赛全国总决赛二等奖

三、指导老师

刘伟峰老师（刘伟峰，博士，中国石油大学（北京）信息科学与工程学院教授，院长，欧盟玛丽居里学者。2002年和2006年于中国石油大学（北京）计算机系获学士与硕士学位，2006年至2012年在中国石化石油勘探开发研究院历任助理工程师、工程师和高级研究师，其间主要研究领域为石油地球物理勘探的高性能算法。2016年于丹麦哥本哈根大学获计算科学博士学位，主要研究方向为高性能稀疏线性代数子程序。他的主要研究兴趣为数值线性代数和并行计算，其中尤其关注稀疏矩阵的数据结构、并行算法和软件。他的研究工作发表于SC、ICS、PPoPP、ASPLOS、IPDPS、JPDC、FGCS 和 Parco等重要国际会议和期刊。他还是 TPDS、SISC 和 TKDE 等多个重要国际期刊审稿人，也是 SC、ICS 和 ICPP 等多个重要国际会议的程序委员会委员；IEEE高级会员以及 CCF、ACM 和 SIAM 会员。

金洲老师（金洲，博士，讲师，IEEE、IEICE、CCF 会员。2010年于南京大学计算机科学与技术系获学士学位，2012年和2015年于日本早稻田大学获硕士与博士学位，此后在早稻田大学研究中心从事博士后研究工作。主要从事晶体管级超大规模集成电路仿真研究、非线性电路和系统模拟验证技术等，尤其关注大规模非线性电路直流分析技术。在DAC、IPDPS、GLVLSI 等重要国际会议和期刊上发表学术论文20余篇，曾参与完成文部省 Global COE 卓越大学院项目、日本政府、北九州和福冈地域创新战略项目等多项模拟电路设计与仿真方向科研基金。先后曾获得日本电气学会九州支部长奖、日本帝人久村财团帝人奖学金、早稻田大学IPS特别奖学金、早稻田大学优秀青年博士奖学金等。她还是ICPP、CLUSTER 等重要国际会议的程序委员会委员。

四、赛题介绍

本次分享的作品题目是由概伦电子命制的赛题：快速电路仿真器（FastSPICE）中的高性能矩阵向量运算实现

概伦电子成立于2010年，是一家具备国际市场竞争力的 EDA 企业，拥有领先的 EDA 关键核心技术，致力于提高集成电路行业的整体技术水平和市场价值，提供专业高效的EDA 流程和工具支撑。公司通过 EDA 方法学创新，推动集成电路设计和制造的深度联动，加快工艺开发和芯片设计进程，提高集成电路产品的良率和性能，增强集成电路企业整体市场竞争力。

五、作品分享

1、摘要

在电路仿真中，根据基尔霍夫电流定律和基尔霍夫电压定律构造的矩阵非常稀疏。由于矩阵的小粒度和实际仿真中的高并发性，因此很难在仿真中加速SpMV。为了解决这个问题，我们提出了一系列的方法，例如判断任务的规则程度，任务合并，单指令多数据集，循环展开，负载均衡，编译器优化和 OpenMP 并行技术，然后将它们组合以获得最佳解决方案。经过多次实验，任务合并，周期扩展，负载平衡，编译器优化和 OpenMP 并行技术的组合是加快问题解决速度的最有效方法。在本实验中，基于实际情况，该模拟器用于模拟各种意外情况， 并提供1024 组稀疏矩阵矢量乘法的 N 次迭代。为了获得稳定性能，通常将N设置为 1024。实验环境是 32 核服务器。并行打开 32 个线程后，代码速度是原始代码速度的11.4 倍。 

2、关键字

SpMV，仿真，任务合并，周期扩展，负载平衡，编译器优化

3、引言

由于大型存储电路（例如 DRAM，Flash，SRAM 等）具有非常多的节点，因此，由于矩阵的维数很大，因此，如果存在以下情况，那么这种高维矩阵将不可避免地消耗大量内存：存储在普通的二维数组中。另外，由于电路中的节点通常仅连接到几个节点，所以电路方程式的矩阵通常是稀疏度高的稀疏矩阵。这使我们可以对稀疏矩阵使用特殊的存储方法，以减少内存消耗并可以存储高维矩阵。

4、项目背景

本次赛题的设计要求为：依照赛题给定的一系列大小不一的矩阵和与矩阵尺寸匹配的向量，用赛题给定的接口完成矩阵向量乘。并在满足正确性的前提下，尽可能用最短的时间和最少的内存把矩阵与向量相乘的结果写到内存指定的位置。包括算法优化、指令集优化和缓存优化等。

5、项目成果

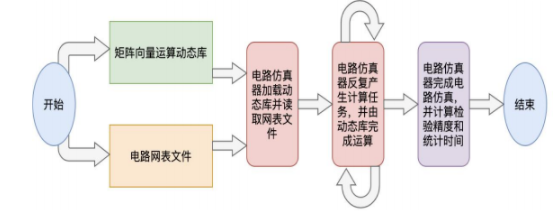
为了解决实际仿真器中的非线性方程组，有必要多次求解稀疏矩阵矢量乘法，并且根据所采用的算法，实验结果产生的误差也有所不同。根据实际要求，经过固定的迭代次数后产生的实验结果误差不能超过 1e-12，以下就准确性和收敛性进行说明。

准确性和收敛性：实验中采用了许多不同大小的电路网络表，较小的电路网络表执行时间约为几百秒，较大的电路网络表执行时间可能是较小电路的数百倍，经过我们的算法多次修改和调整时，无论电路大小如何，经过固定的迭代次数后都可以快速收敛，将误差控制到 1e-12，成功找到正确的答案，具有更好的准确性和收敛性。

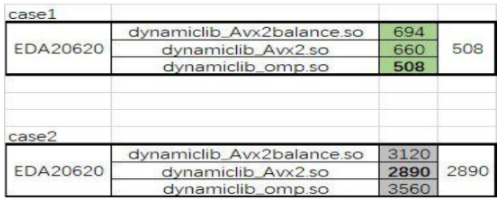
结果表明，该算法可以在 32 核服务器上快速收敛矩阵，并计算出各种尺寸，尤其是大规模的矩阵，这也证明了该算法的实用性和收敛性。另外，通过在整个算法测试期间在 fastspice 仿真器中进行测试，可以进一步提高算法的实用性。

6、主要技术路线、实现方式及创新点

我们已经提出了五种用于稀疏矩阵矢量乘法的加速方法。本部分介绍了这五种算法的核心算法和基本原理。分别是任务合并、单指令多数据集、循环展开、负载均衡以及编译指令优化。

1）任务合并

本次实验的核心算法是提高程序的运行效率，所以我们首先想到的是对程序进行并行化。但是在程序并行化之前，我们首先需要提高程序的串行速度。因此，为了提高 taskB 的串行执行效率，我们在实际模拟中分析了数据处理中使用的公式的特征，发现有些运算不涉及先前运算的运算结果。这些公式中计算所需的向量只需要读取，不发生数据冲突。于是，我们将最初用于实现这五个公式的五个for循环合并为一个for循环；并且，我们还将 const 定义用于程序中的一些常用数据，提高程序的健壮性和效率。 

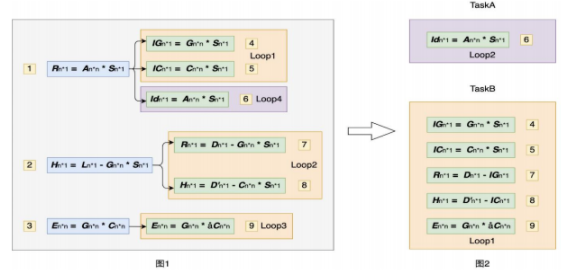
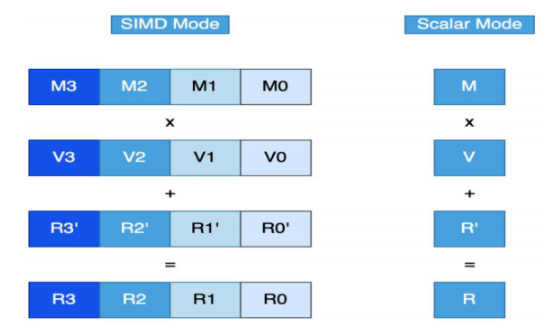
2）单指令多数据集（SIMD）

SIMD 的核心算法是在计算矩阵向量乘法时根据行索引找到指定的行数。若我们要计算的行有多个数据，那么我们使用 SIMD，即数据向量化，这将大大加快程序的运行速度。本次实验中，我们使用 avx2 指令集进行数据向量化。但是，只有在矩阵的每一行中都有大量数据时，avx2 指令集的运行速度才能显着提高。通常认为，向量化处理的数据量要大于 4。

因此，在每次进行向量化之前添加一个判断指令，以检测要计算的数据量是否大于 4。如果大于或等于 4，则使用由avx2 设置的指令操作数据。

例如，我们可以使用_mm256_i32gather_pd（）函数和_mm_loadu_si128（）函数获取数据索引的同时读取 double 数据，再使用函数 _ mm256_ fmadd_pd（）执行乘法和加法运算；如果小于，则将执行常规操作。另外，对于每个运算的spice 矩阵，我们将奇数和偶数数据分开，最后以加法运 算的方式完成整个任务的运算。

3）循环展开

在我们需要加速的任务中，for 循环是最耗时的部分，因此我们的目标是加速程序中的 for 循环或减少程序中的 for 循环。在上一部分中，将程序AVX向量化之后，我们对尚未向量化的数据采用循环计算。但是，for循环大大降低了我们的运行速度。故我们使用循环展开策略来每次计算剩余数据，提高计算效率。

4）负载均衡

如果我们使用普通的并行性，即仅使用 OpenMP 库提供的命令将任务分配给系统，则每个线程分配的任务数量是不同的。我们观察了每个矩阵的任务量，发现某些矩阵有数千行数据，而另一些只有几十个数据。另外，我们也使用 top命令在程序运行时观察每个 CPU 的利用率，有些是 40％，有些是 70％。因此，我们对整个任务进行负载平衡。我们计算每次迭代中每个任务的非零元素数，记录每个任务中非零元素数的前缀和，确定每个线程应平均的非零元素数根据 CPU线程数进行分配，然后根据前缀和确定任务分段的实际边界，再使用 OpenMP进行并行计算。另外，每次运行前，我们会测定变异系数来判断本次运算是否值得负载均衡，若变异系数值较小，我们就不再进行负载均衡。

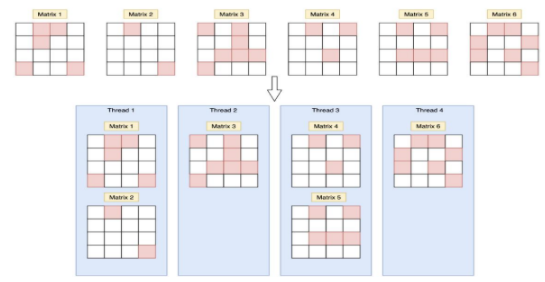
5）编译指令优化

首先我们采取了最基础的优化，分别为：

-O1 提供基础级别的优化

-O2 提供更加高级的代码优化,会占用更长的编译时间

-O3 提供最高级的代码优化

此后，我们又根据程序特点选取了-pipe、-shared 两个优化指令进行优化。 

7、问题及解决方法

问题一：矩阵为稀疏矩阵

解决方案：针对矩阵为稀疏矩阵，所以将矩阵存储为 CSR 格式，我们参赛者只需要根据 CSR 存储的特点，进行相应的运算，就能大大提高运算速度。

问题二：任务颗粒度小但突发执行的次数较多，对响应速度要求很高。

解决方案：由于每个任务的颗粒度小，故我们将并行的分割重点放在了粗粒度的每次迭代总任务的并行运算上，我们将计算每次迭代中，N 个任务的非零元总数，进行负载均衡，提高运行速度。 

问题三：不连续内存访问频繁，效率低下。

解决方案：由于每次运算都是只取部分行列，所以不连续内存访问频繁，效率低下，对此，引进单指令多数据集，即 AVX2 集，以及循环展开，降低了运行速度。

问题四：对运行时间要求苛刻，只能使用效率很高的编程语言。

解决方案：由于算法对运行时间要求苛刻，故采用效率很高的 C 语言进行编程。

问题五：任务运算量可变，需要运算的矩阵的行号和行数都会变化。

解决方案：由于任务的运算量可变，所以在每次迭代前我们都重新计算非零元数量，进行任务分割。

六、团队采访

1、参赛队伍

为了取得更好的加速效果，我们学习了很多关于高性能计算的知识。同时，我们也感叹原来仅仅只接触到了 EDA 行业的冰山一角。在这次比赛中，我们也发现了我们的一些不足，局限于自己对计算机系统的了解，我们队伍完成这个赛题所采取的方法主要集中在算法层面的优化，而对于高效内存同步机制、高速缓存优化等系统层面的优化却寥寥无几；另外，由于这个赛题是从实际应用出发，这就要求我们更加了解工业界电路仿真。博观而约取，厚积而薄发，我们在今后的科研与学习中会更加努力成长，为祖国EDA事业添砖加瓦。 

2、指导老师采访

本次同学们采用了多种高性能算法去完成赛题，这对他们了解 EDA、高性能计算都很有帮助。也锻炼了他们自主学习、找寻知识的能力。为即将进入该领域的年轻学子们提供了一个锻炼成长的机会。祝愿集成电路 EDA 设计精英挑战赛越办越好！ 

3、大赛记忆

参赛过程中，与很多其他学校的优秀同学们进行了密切的交流，也认识了很多志同道合的好朋友，是不可多得的交流学习机会，也是一段让人难以忘怀的回忆。